Transport in Showerhead Reactors: Simplified Analysis
In a showerhead reactor, we usually place the showerhead at the top and a heater with a wafer on it on the bottom. The fundamental problem we are interested in is: how does a precursor chemical we put into the gas stream passing through the showerhead reach the surface? How does the deposition rate depend on the flow, pressure, and size?
If we approximate the showerhead itself as an ideal porous material and treat the flow as incompressible, gases are dispensed uniformly from the showerhead but must move radially to exit at the perimeter.
Thus, at any radius, all the gas dispensed from inside must flow outward (ignoring changes due to reactions in the gas or at the surface). Since the area dispensing increases as the square of the radius, and the perimeter area is linear, the radial velocity of the gases must increase linearly with radial distance: the radial velocity should go as r/2Hc.
With this in mind, let's see what can be learned from an overall examination of transport in the reactor, without taking into account the detailed nature of the gas flow. As usual we approximate the flows using the ideal gas law. In this case (as we'll see) the vertical temperature distribution is linear, so it is reasonable to treat thermal expansion by taking as the approximate chamber temperature the average of the wafer and ceiling temperatures. We assume transport properties for nitrogen as a representative gas. Here are the results:

For the conditions given, the diffusion length is much larger than the ceiling height, so we know that convection plays a weak role in transport in the axial (vertical) direction. The concentrations of precursors and products will be constant or linear in height. For the same reasons, the temperature in the gas phase will be linear in height from the wafer to the cooler ceiling. The residence time is very short: about 10 times less than in the comparable case we examined for a horizontal tube reactor. The combination of a short residence time and confinement of high temperatures to the region near the wafer makes showerhead reactors appropriate for use in systems where high rate gas phase reactions are important. The residence time is linear in the ceiling height Hc; as we noted, variation of Hc is a simple way to influence operation of showerhead reactors.
Radial transport appears to be an issue at this level of analysis: the diffusion length is similar to the radius of the chamber. However, the interested thing about a showerhead is that, if the gases at the showerhead are dispensed uniformly in radius, and the bottom surface behaves in a constant fashion, the boundary conditions are independent of the radial position. Howling et. al.’s 2012 paper [1] shows that in such a case, we only need to think about transport from top to bottom (the z-direction). Basically, what's going on is that, even though the radial velocity is large, if the concentrations are only dependent on z, the stuff carried in is the same as the stuff carried out, so we get to ignore it. All we need to know is: what is the vertical velocity profile of the gases? To find out, we'll start with the simplest possible approach, using incompressible flow and ignoring viscosity. After finding the vertical velocity profile and corresponding distribution of species, we can estimate the deposition rate (assuming we are transport-limited) and the efficiency of precursor use.
Stagnation Flow
It turns out to be pretty simple to derive an analytic expression for the gas velocity in a showerhead-like configuration in the inviscid incompressible flow approximation: that is, we assume the gas is incompressible (also ignoring thermal expansion) so that volume in is the same as volume out, and we ignore the fluid viscosity. These are very similar assumptions to those underlying our plug flow treatment of cylindrical ducts. However, in this case we must account for the presence of an impermeable bottom boundary (the wafer and substrate holder): the vertical velocity must equal 0 at z=0.
We treat the showerhead as a continuous source of gas, ignoring the individual dispensing holes: thus the vertical velocity is fixed at z=(ceiling height). Incompressibility means that the divergence of the velocity field must be zero everywhere: this is a potential flow.

The divergence equation can be written out in cylindrical coordinates (assuming no azimuthal flow):
We assert that the solutions for the vertical and radial velocity are:
These expressions satisfy the boundary conditions: the vertical velocity is equal to -(the inlet velocity) at z=Hc, and is 0 at z=0. The radial velocity is just what we derived at the beginning of this section, by conserving total gas volume. This is known as stagnation flow because the velocity goes to zero in the middle (r=0, z=0).
To prove that this is the correct solution we verify that the divergence is zero, using the chain rule to differentiate the r*v term:
Let us examine the behavior of the solution. The vertical velocity is linear in height, the radial velocity similarly linear in radius. The total fluid velocity at any point is:
For r >> Hc, the velocity is dominated by the radial component, and is just linear in the radial distance, as one would expect.
To make a picture of what this flow looks like, we can derive an equation for the streamlines (paths of test particles trapped in the flow). The path a particle follows is determined by the ratio of the vertical and radial velocities at each point:
We can integrate the equation, since we know the velocities, and find:
which is independent of the inlet velocity vin. The flow pattern looks like this, for a ceiling height of 1.5 cm and radius of 10 cm:
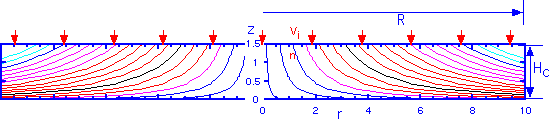
It is interesting to note that we can also calculate the time that a particle -- or a precursor gas molecule -- has spent in the stream since it entered the chamber, for any given position. The answer is
and has the necessary and interesting feature than the time in the stream goes to infinite as the height goes to zero: gas molecules can never actually get to the wafer by pure convection! Diffusion is always necessary for deposition.
Since the time in the stream is only dependent on the height, the time for gas phase reactions is independent of the radial position. This may seem a bit puzzling: one is tempted to think that the gases have been around for longer as we move towards the outside of the showerhead, but the compression of the streamlines towards the bottom of the chamber for larger r compensates. This surprising but simple result is consistent with the assertion above that there is no radial dependence in the idealized showerhead.
To use the solution, we need to know the inlet velocity vin. Recall that standard flows are measured not in volume but in molar units (STANDARD liters/minute = 1/22.4 of a mole per minute). Let's use Fin as the number of moles entering the chamber per second, obtained from our mass flow settings. We divide by the area of the showerhead, Ain, to get the moles per square centimeter coming in. Then we divide by the molar density in the chamber to get the inlet velocity. The molar density can be obtained from the ideal gas law, using the chamber pressure and (average) temperature. So we get vin = Fin /( Ain 𝛒m ).
Convection + Diffusion = Confusion?
Hopefully not. Recalling the discussion above, we're only interested in transport in the vertical direction, so we only need to consider the vertical velocity, which is linear in vertical position from our stagnation flow solution.
As a consequence, we can take a vertical slice at any radial position and examine transport due to diffusion and convection, where in each case we only include transport along the vertical (z) axis. Recall that (in this approximation) the vertical velocity is just linear in position. (In the derivation below we’ll ignore thermal expansion to keep the expressions simpler, just using an average chamber temperature.)
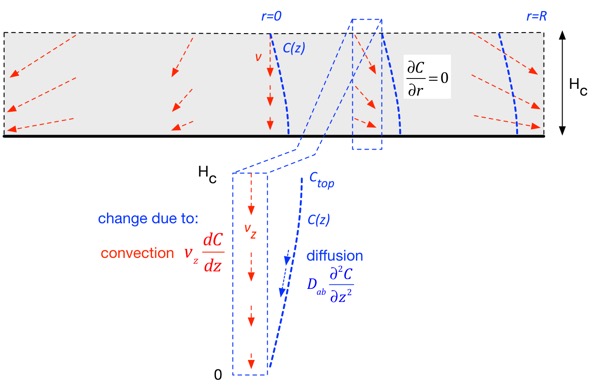
The change in concentration at any location is due to stuff carried in by the vertical (downward) velocity, and is thus proportional to the gradient: if the stuff above us has the same concentration as where we are, convection doesn’t change anything. The net change due to diffusion is the difference in the flux in and the flux out, both of which are proportional to the gradient in concentration, so the change is proportional to the second derivative of concentration. The net result in steady state is:

which has solutions:
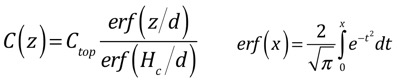
To find the characteristic length, we balance the stuff going in from the top of the showerhead with the stuff that is deposited and carried out of the chamber. Note that we are assuming that deposition is fast and thus is limited by diffusion to the surface, so that the concentration of the precursor at the surface is small. If the deposition is slow, you don't really have to worry about transport, so why are you reading this?
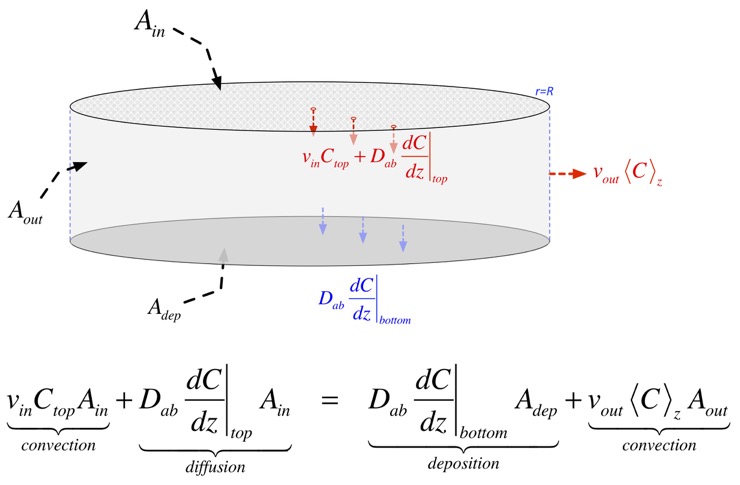
When we do the algebra, we find that the concentration at the top, and all the complicated functional dependences, cancel, and we get a simple answer:
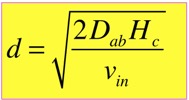
The characteristic length d turns out to be very useful in categorizing the solutions. When d >> Hc, the solution just looks like a line; this is very close to the diffusion solution we examined in the simplified analysis. When d <<Hc, we can divide the solution into two nearly-linear parts, for regions z<d and z>d:
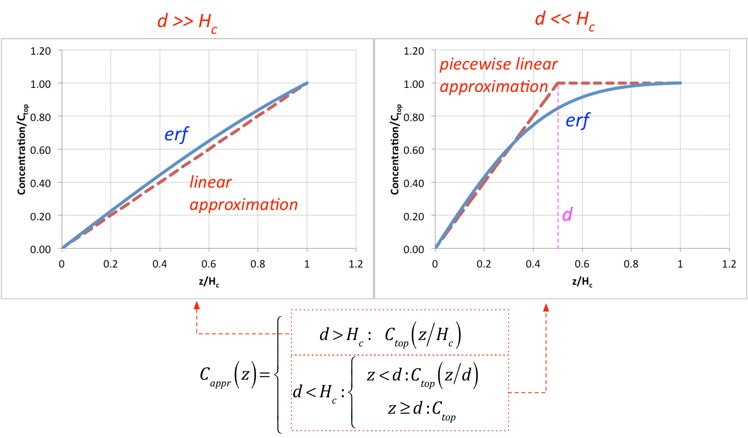
This is great, but to use the solutions we need to know what the concentration at the top (z=Hc) is. One's first impulse would be to say: isn't the concentration at the top of the chamber just the concentration of stuff we put in? But here we have to think more carefully about a real showerhead. An actual showerhead is typically composed of an array of small holes (e.g. < 1 mm in diameter) separated by much larger than their diameter, so that the holes constitute a small percentage of the area. After gases exit the holes, they rapidly slow and spread out, so that transport is all convection inside the hole but diffusion plays a much larger role as we move away. Usually the height of the chamber is significantly larger than the hole separation, so through most of the chamber we can ignore the presence of the holes and assume flow is uniform. However, to do this we need to use an effective concentration at the top of the chamber, because as the gases spread out from the holes, the concentration of e.g. a precursor may change if diffusion towards the substrate is important.
To find this effective concentration, we conserve species. The concentration of precursor that goes into the chamber through the showerhead must be the same as the precursor leaving the top region to travel through the chamber. We have to include the chamber pressure (through the molar density there) because it is often very different from atmospheric pressure, but for simplicity we can ignore thermal expansion. We can then estimate the amount leaving the top and set it equal to the amount entering:

After some algebra we find an expression for the concentration at the top. We can approximate this and obtain the deposition rate and the precursor efficiency in the two cases where d is large or small compared to the height of the chamber, as shown below.
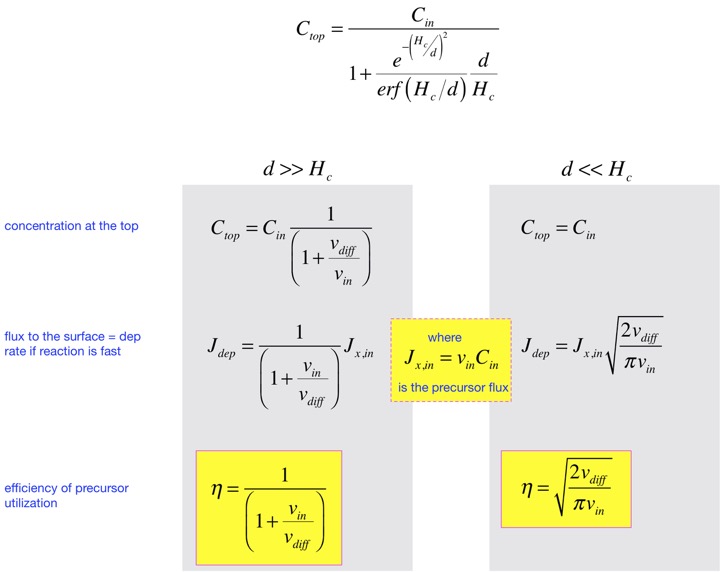
That is: when the input velocity is small, diffusion dominates and efficiency is close to 1, but the concentration at the top is not very high, and the deposition rate is small. If we turn up the gas flows to increase the rate, we reach a regime where the rate goes up less than linearly in the gas flow, and the efficiency of precursor utilization falls. The price of rapid deposition is waste of the precursor.
The plot below shows how the deposition behavior changes, for conditions similar to those examined n the overall transport example we started with (except for a reduction in diffusion coefficient to make the change a bit more visible). We see that at very slow flows the transport length d is large. The deposited flux is close to the input flux, and efficiency of utilization of the precursor is close to 100%, but at the cost of a low concentration at the top of the chamber and slow deposition rate. As we turn up the total flow, the concentration at the top of the chamber approaches the input concentration. The deposition flux increases, but not as rapidly as the input flux, so efficiency of precursor utilization falls. Going faster is not free. This is essentially the stirred reactor / differential reactor problem we examined in our overall transport analysis: you can wait long enough to be well mixed but go slowly, or go fast but suffer gradients in the reactor. Real semiconductor chambers typically operate in moderately-diffusion-dominated regime, where some efficiency is sacrificed for higher productivity.

Details Part 3: What About Viscosity?
Can we really ignore viscosity? Let's take a look.
Howling and colleagues [1] have provided an explicit expression for the z-velocity in a linear showerhead for the case of creeping flow (small Reynolds number), including viscosity:

A plot of this expression shows that it is only moderately different from the linear approximation we have used in section (2) above:
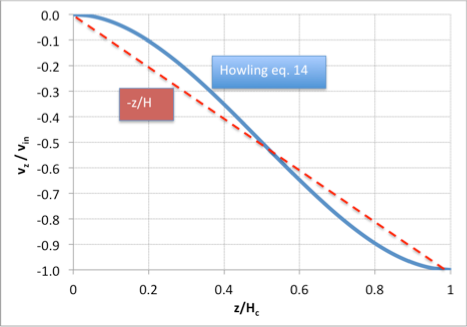
However, the radial velocity is parabolic rather than constant with z. As long as species concentrations don’t vary much with radius we can get away with ignoring this fact, but it becomes important if we need to account for the origin of streamlines within the reactor.
================
References:
1: ”Plasma Deposition in an Ideal Showerhead reactor: A two-dimensional analytical solution“, A. Howling, B. Legradic, M. Chesaux and Ch. Hollenstein, Plasma Sources Sci. Technol v. 21 015005 (2012), DOI 10.1088/0963-0252/21/1/015005
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
