Showerhead Reactor Heat Transport
What determines the wafer temperature?
In steady state, the amount of heat flowing into the wafer must equal the amount flowing out. Except at the wafer edges (an important place, to be sure!), the problem is essentially one-dimensional: the heat flows into the wafer from the heated wafer platen, and leaves to the gas and chamber ceiling. The situation is shown schematically below:
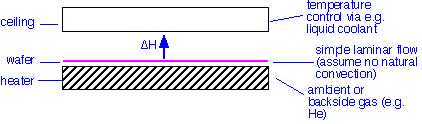
The wafer is heated by conduction through an ambient or intentionally introduced backside gas such as helium. It can radiate to the ceiling and heat the ambient gas by convection and conduction. What are the heat fluxes?
An upper bound on heat loss due to convection is set by assuming that all the gas that goes into the chamber enters the chamber at the ceiling temperature and then is heated to the temperature of the wafer:
For flows of a few hundred sccm this results in heat fluxes on the order of 2-7 W. Note that this result is independent of the operating pressure of the chamber, depending only on the molar flow.

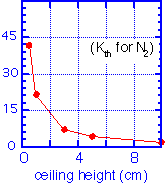
The heat loss by conduction through the gas is:
Note again that thermal conductivity is independent of pressure as long as the mean free path is much shorter than the ceiling height. For a 150 mm wafer at 400 °C and a ceiling temperature of 100 °C, we find total heat fluxes of a few 10's of watts.
The heat loss by radiation is:
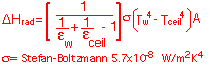
(Note that in this formula the temperature must be in Kelvin!)
We can conclude that the heat loss from the wafer is due to:
Convection only at very high gas flows (many slpm for a 150 or 200 mm wafer)
Conduction if the ceiling height is very small (<1 cm) and temperature moderate (<300 °C)
Radiation if the temperature is > 400 °C or ceiling height is > 2 cm
What temperature is the wafer at? This depends on the heat transfer to the wafer from the heater. A "flat" wafer on a "flat" platen will actually make contact with the platen in only a few isolated places; most of the heat is transferred either by radiation from the heater or by conduction through the gas. The spacing between the wafer and the platen can be assumed to be a few microns to a few 10's of microns for reasonably flat parts; this is less than the mean free path for LPCVD applications, so the heat transport is in the accommodation regime: that is, the atoms strike the wafer or heater surfaces much more than they strike each other. The amount of heat transported per unit area (MKS units!) is:

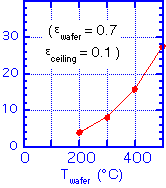
Radiative transfer is the same as above: radiation between two planes. We need to adjust the wafer temperature until the heat flux in equals the heat flux out. Let's look at a practical example. For a gas flow of 300 sccm, chamber pressure of 1.5 Torr, ceiling height of 2 cm, reactor diameter (= wafer diameter) of 150 mm, accommodation coefficient of 0.25, and an aluminum heater (emissivity around 0.1) we find the heat balances:
HEATER TEMPERATURE: 400 C GAS FLOW: 300 sccm CHAMBER PRESSURE: 1.5 Torr CEILING HEIGHT: 2 cm WAFER DIAMETER: 150 mm ACCOMODATION COEFFICIENT: 0.25 EMISSIVITY: 0.1 (heater, ceiling) 0.7 (wafer) WAFER TEMPERATURE: 350 C CONVECTION OUT: < -2 Watts (neglect) CONDUCTION OUT: 11 Watts RADIATION OUT: 12 Watts RADIATION IN: 6 Watts CONDUCTION IN: 16 Watts total:
about 0!
That is, the wafer can be much cooler than the heater! Further, much of the transport is radiative, so changes in the chamber conditions (e.g. coating an initially reflective ceiling with a material such as silicon dioxide, which is fairly absorbtive in the infrared) will change the wafer temperature. The wafer temperature can also differ depending on the emissivity of the wafer, which depends on the doping, temperature, and what layers have been deposited on the wafer. So it is certainly not sufficient to accept a thermocouple measurement of the heater temperature as if it were the wafer temperature; see our discussion of temperature measurement approaches.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
