Convection and Diffusion
- Convective transport occurs when a constituent of the fluid (mass, energy, a component in a mixture) is carried along with the fluid.
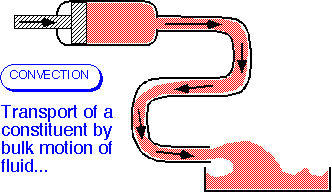
- The amount carried past a plane of unit area perpendicular to the velocity (the flux) is the product of the velocity and the concentration:
J = U*[stuff]
- units:
- (m/sec)*(moles/m3) = moles/(m2*sec) [molar flux]
- OR (m/sec)*(kgm/m3) = kgm/(m2*sec) [mass flux]
- OR (m/sec)*(joules/m3) = joules/(m2*sec) [energy flux]
- ...that is, there can be many alternative ways of keeping track of stuff being transported by a fluid or gas.
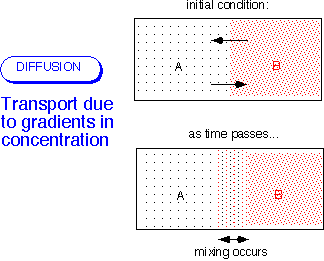
Recall from kinetic theory that the velocity of the individual molecules greatly exceeds the bulk velocity of the fluid for most of the cases we're interested in -- that is, whenever the flow is incompressible, U << (velocity of sound).) In the simplest case, the flux is proportional to the gradient in the concentration of the stuff of interest. As above, it is possible to consider the flux of moles, mass, molecules, etc.: these are alternative views of the same molecular motions.
Note that other gradients (e.g. temperature) can also drive diffusive processes: in the most general case, diffusion arises from the gradient of the chemical potential. Thermodiffusion can be important in CVD processes involving light molecules like hydrogen.]
In the general case, it is necessary to account for both mechanisms of transport. The flux of each component of a mixture is determined by its concentration and both the "bulk" fluid velocity (the average of all the components) and the "diffusion" velocity of the component.
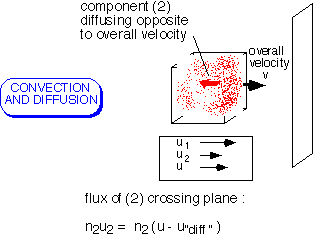
Note that various velocities and fluxes can be defined, depending on whether you wish to count mass, moles, molecules, etc.: all approaches will work as long as they are pursued consistently.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
