Radiative Heat Transfer
Who Ordered That?
The conduction, diffusion, and convective transfer of heat are generally similar to the comparable mechanisms involved in mass transport. However, energy can also be carried by photons. This is radiative heat transport, which has no analog in mass transport.
In a closed system each object at a finite temperature T is in equilibrium with a gas of photons, distributed in frequency (or energy) according to the blackbody distribution discovered by Planck. In a closed system, the amount of energy absorbed from the photon gas is equal to that emitted by each object. The principle of detailed balance allows us to assert that even in an open system, objects still radiate the same amount of energy.
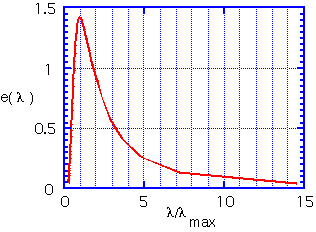
Since the amount of photons at each energy is proportional to the fourth power of the temperature, the total heat energy emitted per unit area of surface is proportional to the fourth power of temperature;σ is the Stefan-Boltzmann constant.
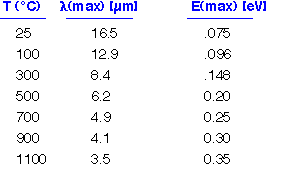
The peak in the distribution is at an energy of about 3 kT. The radiated energy is in the far infrared at room temperature. Even at 1000°C, where objects appear to glow brightly, most of the energy is still being emitted in the mid-IR. (3.5 microns is a typical wavelength for e.g. the vibration of O-H bonds in water).
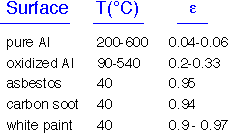
Real objects reflect some of the energy impinging on their surfaces. In order to maintain energy balance fin equilibrium, these objects must also emit less: that is, the energy emitted is multiplied by an emissivity <1. Kirchoff's law says that the emissivity must equal the absorbtivity at each wavelength; we can often ignore wavelength dependence and set emissivity = abosrptivity.
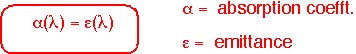
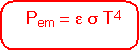
Highly reflective objects have emissivities near 0; "dull", black objects have emissivities near 1. Some typical emissivities are shown here. Note that white paint has a high emissivity: it is reflective in the visible but not in the IR!
The full treatment of radiation can be extremely complex, since photons can reflect off multiple surfaces and follow complex paths. We'll examine only simple planar geometries to get some sense of what sort of heat fluxes occur in typical situations.
How do conduction and radiation compare in importance? Radiation is essentially independent of spacing, whereas conduction is strongly dependent on spacing.

Here we show calculated fluxes in the simple case where the upper (cool) surface is a pefect black absorber, held at room temperature. For a spacing of about 0.1 mm the two fluxes remain comparable over a wide range of temperatures. Of course, if the plate separation is increased the conducted flux falls rapidly whereas radiated flux is essentially unchanged.
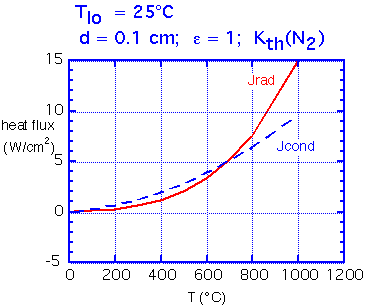
Typical radiative heat flux varies from 1-2 W/cm2 at 200°C, to around 10 W/cm2 at 900°C.
When surfaces are not perfectly absorptive, calculation of the net heat flux from one surface to another is rather subtle. One must account for the energy reflected from each slab, and either sum multiple reflections using the geometric series (1 + x + x2 + ... = 1/[1-x]), or by requiring consistency of energy fluxes.
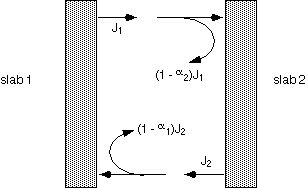
The final result contains a term of the form T14 - T24, as would be the case with simple black objects. The coefficient dependent on emissivities is rather complex: let's look at a few special cases.

When both objects are perfect absorbers, the net heat is just the difference of two blackbody terms. When one emissivity is small and the other close to 1, the smaller emissivity dominates the net flux. When both are comparable but small, they combine in same fashion as two resistors in parallel.
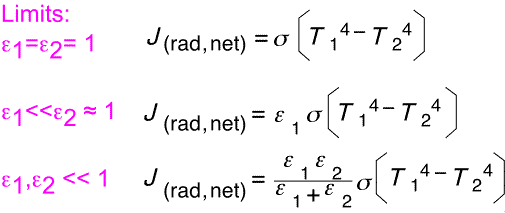
The most common instance of this type of heat transfer in CVD is of course the heating of a flat wafer or substrate. Using the simple treatments presented so far, we can estimate heat flux to a wafer sitting on a chuck, and heat loss by radiation and convection through a thermal boundary layer to a flowing gas on top. We should note that complicating such a calculation is the complex emission behavior of silicon: bare silicon is rather transparent in the IR if low-doped (resistivity > a few ohm-cm), but becomes absorptive (emissivity about 0.7) when heated enough to reach intrinsic conductivity, typically about 300°C. Wafers with thick oxide are usually quite absorptive due to strong O-H absorptions are 3 microns and the intrinsic Si-O absorption around 10 microns. Thus wafer optical properties vary depending on temperature, processing history and resistivity. A useful reference on this issue is Ravindra et al IEEE Trans Sem Manfr vol. 11 p. 30 Feb 98.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
