Pressure, Size, and Knudsen Number
Effect of Pressure
Recall that the mass diffusion coefficient D varies roughly as 1/P, where P is the total pressure. It is often assumed that therefore the effects of diffusion must naturally increase as the total pressure is lowered. However, the residence time also changes: the volumetric flow at a constant temperature and constant molar flow increases as 1/P as well. Thus the residence time is proportional to P. The diffusion length, which contains the product D*t, thus goes as (1/P)*(P) -- that is, the diffusion length is independent of total pressure! The Peclet number is of course also independent of pressure. The Reynolds number depends on the ratio of the velocity and the kinematic viscosity. Since the viscosity is roughly independent of pressure, and the density is linear in P, kinematic viscosity goes as (1/P), and thus Re (1/P)/(1/P) is again independent of pressure.
So why does everyone assume that reducing pressure is useful to increase diffusion? The critical quantity that IS pressure-dependent and very relevant to CVD is the Thiele length: it contains the ratio of D (which goes as 1/P) to the surface reaction rate constant, which is independent of pressure (more or less -- see the discussion of surface chemistry for more details). Thus as pressure falls, the Thiele length grows large, leading to improved uniformity (but reduced absolute deposition rates, since the absolute concentrations are lower).
See the Plug Reactor model page for a more detailed discussion of these issues.
Limits of Continuous Models
When the pressure falls low enough, the continuous transport models we've used no longer apply. If the mean free path:
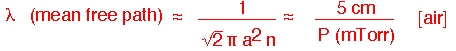
becomes comparable to the size of the chamber, molecules are just as likely to hit the walls as they are to hit each other.
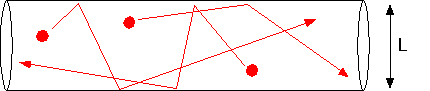
In this case, the diffusion constant takes on a limiting value D(Knudsen) = cL/3, where c is the mean thermal velocity of the molecules. The ratio of the mean free path to system size is the Knudsen number; when Kn <<1 our continuous approximations are valid, and when Kn >> 1 it is necessary to use Monte Carlo calculations (estimates of actual molecular trajectories) to make accurate calculations. One can get order of magnitude estimates by thinking about throwing baseballs in the chamber geometry, but that's beyond the scope of this page!
[Thanks to Sirisha Govindaraju for correcting my definition of Kn. DMD11/04]
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
