Natural Convection
When heat is added to a gas, it expands, and thus changes density. If gravity is present (i.e. pretty much all the cases we're interested in!) this change in density induces a change in the body forces, and the forces may cause the fluid to move "by itself" without any externally imposed flow velocity. This is the phenomenon of natural convection, ubiquitous in our daily experience: rising clouds of cigarette or campfire smoke, ripples of heat from a car's hood, thunderheads reaching into the stratosphere. Natural convection is usually very undesirable in a CVD reactor, since it represents an uncontrolled gas flow. We won't try to deal with the full complexity of natural convection flows, but will treat a particularly simple geometry to illustrate the typical sorts of quantities that arise, and how to estimate whether natural convection is likely to be important in a given configuration.As in our treatment of boundary layer flows, we consider a flow composed of a "free stream" region, in this case with a constant temperature and density as well as velocity, and a relatively narrow thermal boundary layer over which temperature, velocity, and density change. [In the general case one ought to consider two boundary layers one for velocity and one for temperature; however, most gases have similar momentum and energy diffusion rates so we simplify things a bit.] We introduce the modulus of thermal expansion to relate the density to the change in temperature.
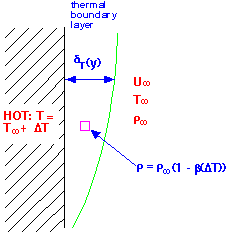
To estimate the velocity, we balance the heat carried through the boundary layer of height H by convection (i.e. transport up) with diffusion of heat into the boundary layer (i.e. transport to the right): in steady state these must be equal. We thus obtain an expression for the velocity in terms of the boundary layer thickness.
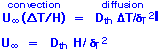
We then balance the force due to buoyancy (in a region of unit depth and height in the boundary layer) with the frictional force, to obtain an expression for the boundary layer thickness.
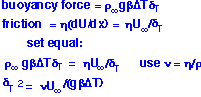
By combining these expressions we obtain the boundary layer thickness and velocity. These can both be expressed in terms of another dimensionless number: the Rayleigh number Ra, in this case based on the height of the region of interest.
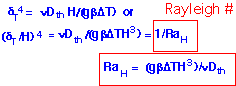
Thus, to figure out if natural convection is significant in a chamber, calculate Ra for the system. If the natural convection velocity is much smaller than the "forced convection" fluid velocity calculated from known inlet flows, then natural convection can be safely ignored. In the other extreme, fluid flow in the reactor is dominated by natural convection, likely leading to recirculations, powder formation due to long residence times in the gas phase, and other undesirable results. We can see that the velocity is strongly influenced by the height: to avoid natural convection in practical situations, make reactors short!
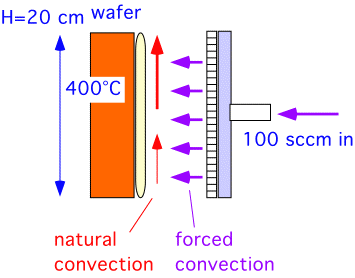
Let's consider an example...
Consider a single-wafer geometry, turned sideways (to resemble the case we studied)...
We note that it is easy to find the modulus of thermal expansion for an ideal gas:
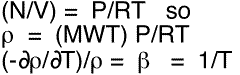
We can therefore find the values for the natural convection velocity and compare them to the inlet velocity (assuming simple volume expansion and plug flow). If the natural convection velocity is much larger than the inlet velocity, natural convection will dominate (and the reactor won't work very well); if the inlet velocity is larger, the forced convection will "blow away" natural convection. Here are the results:
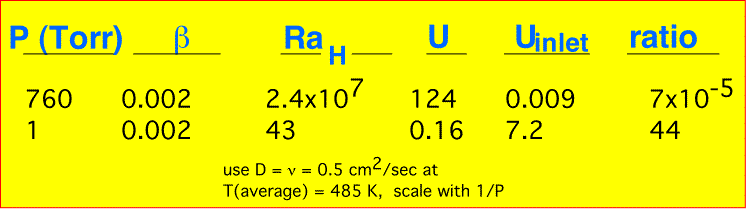
At high pressures natural convection is completely dominant in this geometry; at low pressures forced convection wins. Naturally the result is quite sensitive to the actual size of the chamber (and also, though not included here, to the separation of the gas injection and the wafer: when that is comparable in thickness to the thermal boundary layer, natural convection has too little room to occur and is suppressed).
Note that the situation is somewhat different in the "boiling water" geometry: a large flat cylinder with a hot bottom and cool top. In this case there is no convection at all until Ra reaches a value of about 2000, after which convection cells, of diameter roughly equal to the system height, begin to form.
Prehistoric CVD
Some early CVD reactors (Hugle Rotox, Tempress Pyrox) were based on R&D bell-jar configurations and were relatively tall, with a hot susceptor on the bottom and a gas dispenser on the top. Flow in these reactors was strongly influenced by natural convection and led to serious particle formation problems and poor film quality. Such reactors are now of mainly nostalgic value, except as a warning of what to avoid!
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
