Daniel M. Dobkin

Convection: Fluid Flow and the Reynold's Number

Fluid Flow Made Simple: Ignore (almost) Everything

Mass transport can occur due to motion of the bulk fluid or gas, whether or not concentration gradients exist: that is, through motion of the fluid containing the stuff of interest. Anyone who has ever watched a smoker exhale or a leaf fall in a breeze knows this can be a very complex field! However, in many cases of interest for chemical vapor deposition flows are fairly simple (necessarily, as otherwise the machines could never be made to work!). How do we tell what sort of flow we're dealing with?

The first clue is the Reynolds number.
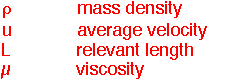
When Re is small (less than about 10), flows are typically very smooth: the "streamlines" (paths of imaginary test particles in the fluid) lie in neighboring layers or laminae, giving rise to the description of this "laminar" flow.
As Re grows large (hundreds to a few thousand) flows become more complex: first recirculations and vortices appear (in which the local velocity is opposed to the global average) ...
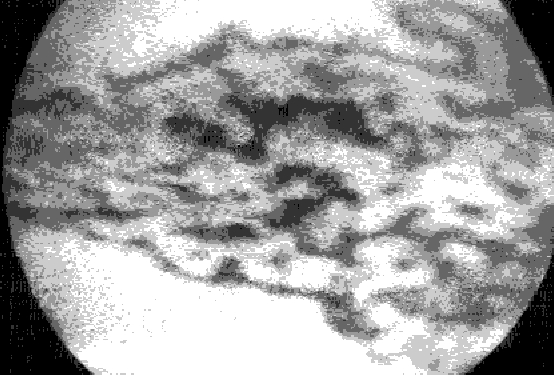
At high values of Re (thousands to millions) flow is complex and unpredictable in detail: turbulent.       [The images of flow shown here are taken from the excellent book "Flow Visualization (2nd ed.)", W. Marzkirch, Academic Press 1987; we didn't get permission but since we don't charge to view the site we hope they consider it either fair use or advertising for the book.]

What is Re? (a physicist's view)

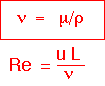
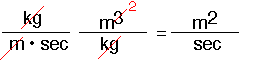
To figure out the physical significance of this obscure combination of parameters, it is first useful to introduce the kinematic viscosity: the viscosity divided by the density:	Note that the kinematic viscosity has the dimensions of a diffusion coefficient: It is interesting to note that it is also numerically of the same order as binary diffusion coefficients for gases: i.e. around 0.1 to 1 cm2/sec.
If we treat it as a diffusion coefficient, then we can calculate a diffusion length, using the residence time L/U:
We then find that the Reynolds number is the square of the ratio of the system size to the diffusion length for momentum: Re is the Peclet number for momentum.

We can now see that small Re corresponds to diffusion lengths comparable to system size: just as before, gradients (in this case in velocity ) are small, and the system behaves as a single unit. When Re is very large (flows with Re > 10,000 or even > 1,000,000 are common in the real world, though fortunately not in CVD reactors) diffusion of momentum only proceeds locally within very tiny cells, and huge gradients are possible: i.e. recirculating and turbulent flows.

Transport: Table of Contents

Go Home