Heat Conduction and Diffusion
As in the case of mass transport, the flux of heat is proportional to the gradient in temperature in simple conduction.For time-dependent conditions we can set the change in temperature in a region equal to the net flux in divided by the heat capacity of the region and obtain as in mass transport a diffusion equation:
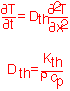
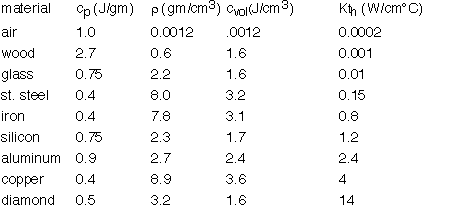
The thermal conductivity varies tremendously between different materials. The heat capacity expressed in molar terms is roughly constant, but in volumetric terms it differs tremendously due to the variation in density between e.g. gases and solids. Some useful values are summarized below:
In steady-state (dT/dt=0) the solutions of the diffusion equation are linear when the diffusivity is constant. However, since Kth varies so much, big differences in slope occur as heat travels through different materials.
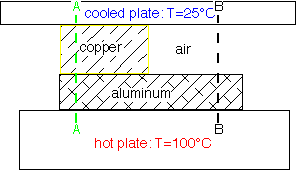
For example, air is such a poor thermal conductor [IF it isn't moving!] that most of a temperature gradient will occur across an air space with very little in surrounding good conductors such as metals. The cross-section B-B at right shows this effect: the aluminum is essentially isothermal with all the temperature drop across the air gap.

Return to Tutorial Table of Contents
Book version of the CVD Tutorial
