Kinetics: The Slowest Step Wins
Reactions and Mechanisms
In our discussion of thermodynamic equilibrium, we dealt with several overall reactions for CVD. The ability to write an overall reaction tempts one to think that the mechanism by which the reaction proceeds is somehow related to the form of the overall reaction, but this is a temptation best resisted. The reaction 2 H2 + O2 => 2 H2O does not proceed through the meeting and spontaneous rearrangement of three molecules into two: in fact, it is a branching radical chain reaction, which is why hydrogen-filled dirigibles were a bad idea.
AN OVERALL REACTION
A + B => AB
DOES NOT IMPLY
Rate = k [A] [B]
In most cases, a reaction has many steps, with one or two often slower than the others and therefore dominant in determining the rate of reaction. As a consequence, the dependence of reaction on the concentrations of reactants and products -- the rate expression -- is often of a complex and non-obvious form.
The order of the rate expression is the sum of the exponents on the concentrations. A rate which is linear in concentration is first order, a quadratic dependence is second order, etc. A complex expression like the one below might be appear to be first, second, or third order overall depending on the concentrations and the values of the constants k.

The coefficients k are usually of an Arrhenius form.
Ea is the activation energy of the coefficient, and is often identifiable with the energy barrier for some actual process, e.g. breaking of a bond, to occur. (The coefficient A may also have some weaker temperature dependence -- e.g. as T2 -- though for large Ea this is swamped by the exponential term.)
The underlying reason why mechanism is so important is that the barriers to a reaction can be very high: to break a bond (often a precondition to making a new one) can require hundreds of KJ/mole, compared to thermal energies of e.g. RT = 2.7 KJ/mole at room temperature. Small changes in the height of the barrier (typically written as the activation energy Ea of the reaction) make a big difference in the probability of a molecule making it over to the next step.
__________________
EDITORIAL COMMENT: In the CVD literature one will often find arguments that proceed as follows "We find that the rate of reaction for this process is (nth order) in reactant (A). We looked at all the mechanisms we can think of and only mechanism (2) is (nth order) in A, so this must be mechanism." The present author recommends that such claims, unless supported by actual microscopic or other evidence, be disregarded: the data for overall rate of deposition is rarely good enough, or acquired over a sufficiently wide range of concentrations, to support such assertions.
The same goes for activation energies: it is all too often the case that a plot showing rate data to be linear on a logarithmic scale vs. (1/T) is taken as evidence for an activated reaction, when in fact the temperature range is so narrow that the data can also be plotted as a linear graph vs. the temperature T and also be linear!
The right answer is the same as in all of science: a theory should only be taken seriously when it can predict the result of observations distinct from those that went into its formulation.
__________________
Transition States
In principle, one can determine the mechanism of a chemical reaction by following the motions of all the atoms involved throughout the reaction. However, it is often simpler to think of the reaction as being relatively independent of the exact path, but involving the passage from the reactant state through a transition state: the lowest-energy "pass" through the configuration space to the products. In an association reaction (that is, a reaction whose net effect is the joining together of two formerly separate molecules) the two molecules might strike each other in the gas phase, A + B => AB*:
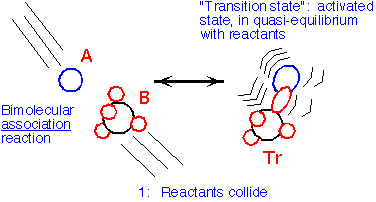
When we conserve momentum, we are forced to convert much of the kinetic energy of the reactants into internal energy of the transition state: this energy will usually cause the reactants to dissociate again, unless a third atom or molecule (often denoted as M), collides with the transition state and takes some of the energy away, allowing association to occur: AB* + M => C

A consequence is that association reactions in CVD (e.g. the starting point in formation of powdery junk in the reactor!) often depend on de-activation by third species. Thus, at low pressures the rate goes down as P3! Once de-activation is rapid (high pressure) the rate becomes "pseudo-first-order", no longer dependent on total pressure. Dust is less likely in LPCVD than in APCVD.
The key to the transition-state approach is to assume that the occupation of the transition state is determined by a "quasi-equilibrium" with the reactants, independent of the exact path between the reactants and the transition state.
The coefficient K is of the same form as a conventional equilibrium constant. (RT/P) is just the inverse of total density, from the ideal gas law: this term makes the dimensions come out right:
[concentration] = (1/concentration)*[conc]2.
Since G = H - TS, this expression can be decomposed into a part determined by the "height" of the barrier (a part associated with e.g. bond breaking), and a second part which essentially shows how many identical states the transition state is composed of (an entropy part).

The overall rate of reaction is then obtained by multiplying the transition state concentration by a term of order (kT/h) describing the frequency of thermal vibrations. (The quadratic temperature dependence here is the theoretical justification for the T2 terms often encountered in empirical rate expressions.)
Rate Expression Example: Unimolecular Decomposition
Now that we've given some thought to the origin of the k's in the rate expression, let's look at how a seemingly simple reaction -- say the simplest sort one could imagine, A => B + C -- can give rise to a complex rate expression. This very simple reaction, if taking place in the gas phase, is likely to consist of several steps.
The first step might be excitation of the molecule: a collision with another A molecule, or some other species in the gas phase, gives the molecule of A enough energy to change state. If we assume that only A is present, the likelihood of the reaction is the likelihood of two molecules of A coming together, and is thus proportional to the square of the concentration of A.
A + A => A* + A
Once the excited state is formed, it has two alternative paths to follow. It could collide again, giving away its energy and returning to the ground state. This process contributes a change in [A*] proportional both to the concentration of A* and to the background concentration of A molecules which can remove the energy of excitation.
A* + A => A + A
Alternately, the excited state could decompose into the product molecules. This "unimolecular" process is just the result of random vibrations within the molecule, and its rate is only dependent on the concentration of excited A, [A*].
A* => B + C
The overall change in the concentration of A is the sum of the three terms corresponding to excitation, de-excitation, and decomposition. Now we make an important approximation frequently employed in kinetics: we assume that we are in a steady state condition, so that the concentration of the intermediate species A* doesn't change in time.
We can then solve for the concentration of A*:
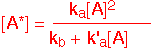
Plugging this value into the expression for the rate of decomposition (which is also the rate of production of B or C) we obtain a Lindemann-Hinshelwood reaction rate law:
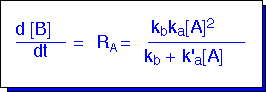
Note that such a rate law can behave differently in differing conditions. At low pressures, de-excitation might be relatively slow (i.e. k'a*[A] << kb): the rate of reaction becomes second-order in A:
At high pressures, de-excitation might be very fast (kb small), and the reaction becomes "pseudo-first order”:
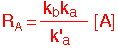
We see that even a very simple reaction can result in pretty complex behavior. So you can imagine what a mess you can get when there are lots of competing paths and multiple species involved.
Radicals: Not Just for Politics Anymore
So far we've imagined reactions in which one molecule hits another and somehow an activated complex is attained, from which the desired product results. It is an obvious generalization to imagine a reaction taking place in several successive steps of this nature. However, if the activation energies for each step are high, reaction rates are likely to be slow: each step is very unlikely to occur, since energies much greater than the thermal energy kT must be concentration in the transition state. To get fast reactions we need some sort of catalysis: a mechanism for lowering the energy barriers of the reactions.
One important path in gas phase reactions is through radicals. A radical species is an atom or molecule with an odd number of valence electrons. Since covalent bonds use pairs of electrons, this is equivalent to saying that a radical has a broken bond: a half-filled orbital. Since a bond must be broken to create a radical, the concentration of radical species is almost always very low. Nevertheless, they can exert a profound effect on reaction kinetics for two reasons. The first is, of course, that they are very reactive, since the half-filled orbital can easily suck up an electron from another bond. The second reason is the simple arithmetic statement: odd + even = odd. When a radical (odd number of electrons) interacts with a saturated molecule (even number of electrons), the result must contain some species with an odd number of electrons: another radical. This new radical is free to react again. A single radical may initiate a chain of thousands of reactions before it is finally consumed either by striking a solid surface, such as a wall, or by meeting another radical: a rare event, proportional to the square of the already small concentration.
A typical radical might be a hydrogen atom
or a hydroxyl (OH):

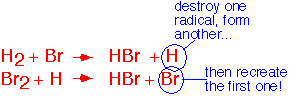
A classic example of a radical chain is the reaction of hydrogen with bromine. The overall reaction looks disarmingly simple:
and one might at first imagine that it proceeds through a collision of a hydrogen molecule and a bromine molecule. The actual mechanism is a radical chain consisting of three distinct steps:
Chain Initiation:
a rare even in which radicals form...
Chain Propagation:
the radical attacks a molecule of hydrogen, releasing another radical (H); the H atom attacks a molecule of bromine, releasing one Br radical. The net effect is to product two molecules of HBr and regenerate the initiating Br atom.
Chain Termination:
At very infrequent intervals two radicals will encounter each other, recombining to recreate the original stable molecule. Note here we have written "M" to indicate a third body required for de-excitation and recombination.
If a step in the chain results in the creation of more than one radical out for a single radical in, the reaction is a branching radical chain. In this case, the number of radicals increases with each iteration, and thus the speed of reaction can rapidly accelerate. If the reaction is exothermic, an explosion will result! The explosion of hydrogen and oxygen is a branching chain reaction. So is the reaction of silane (SiH4) with oxygen to make silicon dioxide, explaining its potentially explosive nature. The pyrolysis (thermal decomposition) of the organic parts of organometallic precursors are also often radical reactions.
Once a chain reaction is initiated by the formation of radicals, the rate of the subsequent steps is not very dependent on temperature, since radicals are so reactive that there is typically little or no activation energy associated with their reactions. Thus radical reactions can be insensitive to temperature over wide ranges.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
