Diatomic Molecules as Examples of Bonding
Let's look at a few diatomic molecules to understand how bond orbitals are put together. We'll look at the first row of the periodic table where only s and p orbitals are important. The energies of the s and p are no longer the same in these multielectron atoms; the diagrams will show this qualitatively but don't purport to accurately represent the value of s-p splitting for each atom. To make bonds, the atomic orbitals are combined into molecular orbitals. Two single-electron orbitals, one from each atom, can be combined to make two possible states: typically one is lower in energy than the original orbitals (the "bonding" orbital) and one is higher in energy than the original (the "antibonding" orbital, denoted with an asterisk *). The bonding and antibonding orbitals are also usually denoted σ or π depending on whether the axis of electron density is along the axis between the nuclei or perpendicular to it, respectively.
Once we have constructed the possible bonding and antibonding orbitals, we simply fill them up with two electrons per orbital until we use up all the electrons in the valence shell of the two atoms.
Molecule Building Practice
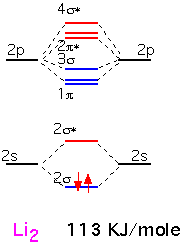
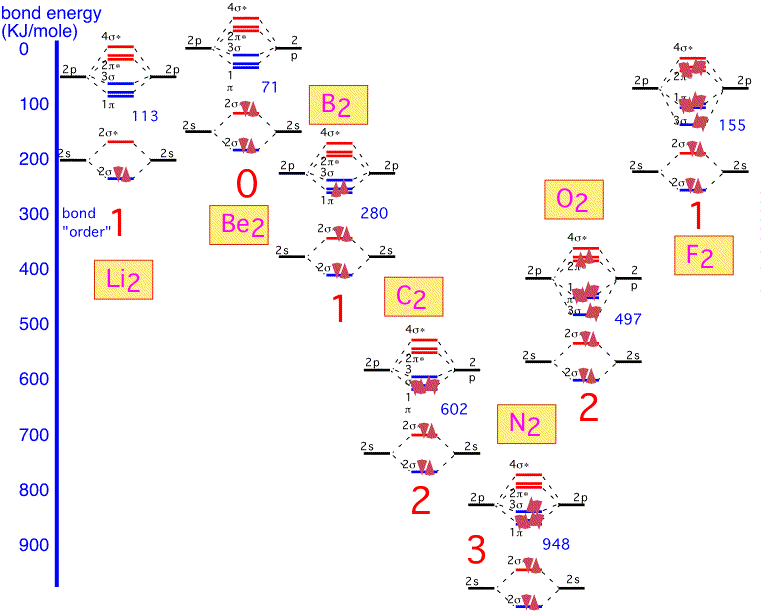
Lithium is the simplest diatomic molecule after H2. We ignore the 1s electrons, which are too close to the nucleus to contribute to bonding. We can make one bonding and one antibonding orbital from the two 2s atomic orbitals. The 2p orbitals allow us to make 3 bonding states and three antibonding states. One of the bonding states has the two p orbitals "pointing" at each other (e.g. px orbitals if the two nuclei are on the x axis); the other two orbitals are made from py and pz, at 90 degrees to the internuclear axis. Thus these two are degenerate by symmetry. The antibonding orbitals are made from the same pairs of orbitals but with opposite signs on one atom, and have a node (plane of zero electron density) between the nuclei.
We thus obtain 8 molecular orbitals, 4 bonding and 4 anti-bonding. Since each lithium atom has only 1 valence electron, we put the two molecular electrons into the lowest lying bonding orbital. We can imagine that we've filled one "bonding" orbital with a pair of electrons: this molecule has a "single" bond. The energy of dissociation (bond energy), that is the energy required for the reaction Li2 => 2 Li, is given in KJ/mole.
Beryllium is the next element in the first row. The molecular orbitals are built in the same fashion, but there are two additional electrons which must go into the anti-bonding (2σ) orbitals. We'd expect the bonding energy to be reduced as a consequence, generally consistent with the bonding energy of about 71 KJ/mole, considerably less than that of Li2.

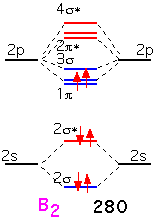
Boron has two additional electrons to add. These electrons go into a bonding π orbital, making the bond energy larger than that of Be2. The strength of the bond (280 kJ/mol) is noticeably larger than the "single" bond in Li2: this is the result of the 2p orbitals, which extend farther from the nucleus and thus overlap more than the 2s. Note that the two electrons are added into separate orbitals to maximize total spin (triplet state) and minimize energy (Hund's rule).
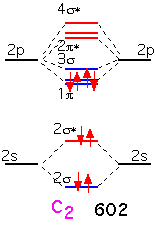
The two additional electrons in carbon fill all the bonding π orbitals. We can look at this molecule as having a "double" bond: a net of two pairs of electrons in bonding orbitals. The bonding energy is much higher than that of Li2.
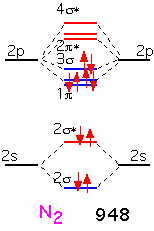
With nitrogen, the remaining (sigma) bonding orbital is filled: there is a "triple" bond. The binding energy is very large indeed: molecular nitrogen is very difficult to dissociate! This is why it is widely used in chemical vapor deposition as an inert gas, even though the nitrogen atom is highly reactive and readily incorporated into many substances.
When we form O2, the two additional electrons over N2 go into antibonding states: the oxygen molecule has a net double bond, and is more weakly bound together than nitrogen. The bonding is still very strong: even though oxygen can participate in many reactions that release a lot of energy, O2 gas is relatively inert at room temperature due to the difficulty of dissociating the molecule into its constituent atoms.
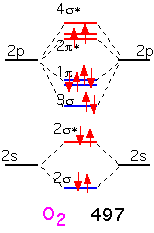
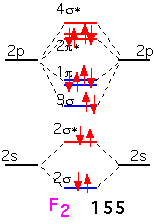
In fluorine, the filling of an additional antibonding state means that the molecule has a net of only one bond: F2 is very weakly bound and hence highly reactive (and dangerous!).
It is clear that if we tried to make a similar diatomic molecule with neon, we would fill all the antibonding orbitals, and have a net "bond order" of 0: neon is inert and doesn't form diatomic (or any other) molecules.
A graphical summary of the discussion is shown below; we can see how the bond order (single / double / triple) qualitatively predicts the bond strength of first-row diatomic molecules:
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
