Equilibrium: Where Things are Going (but who knows when they’ll get there...)
Once we've gotten the required precursors into the vapor phase we can ask whether they can do anything useful: that is, could any chemical reactions occur to produce a solid? The answer to this question has two pieces. The first, the thermodynamics, examines what the eventual equilibrium state of the system is: can the precursors and other gases and surfaces in the system react to form anything else, or are they already as stable as they'll get? The second piece, kinetics, is the examination of how long it would take to actually get anything to take place, and whether the equilibrium state is ever reached.
Thermodynamics, while hardly trivial, is much easier than kinetics to get results out of (although the basic data -- heat and entropy of formation--is surprisingly hard to find for many substances of interest in CVD). So let’s take a look at...
The Equilibrium State
In our discussion of volatility, we used the fact that the equilibrium vapor pressure of a gas over its condensed phase is determined by minimization of the free enthalpy (Gibbs free energy). This result is not unique to evaporation; the equilibrium state of any chemical system -- the concentrations of reactants and products that will be present if you wait long enough -- occurs when the free enthalpy G has reached its minimum value. This is equivalent to saying that the change in free energy due to any reaction (involving a small number of moles) at the equiibrium concentration is 0
For any single reaction like
nA + mB => pC + rD
we can define a free enthalpy of reaction for the reactants in their standard states. The standard state is typically 1 atmosphere partial pressure for a gas at 25 °C. A pure liquid or solid is the standard state of the relevant substance. The free enthalpy for the reaction of n moles of A (and appropriate quantities of the other constituents) can be often be found from standard tables, since it is just the sum of the standard free enthalpy of formation for all the constituents A, B, etc. multiplied by the appropriate stoichiometric coefficients.
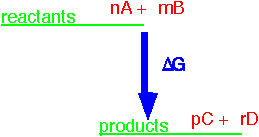
We can find the equilibrium state of the reaction from the equilibrium constant:
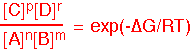
General remark #1:
Gases have much higher entropy than solids; since CVD is the formation of a solid from a vapor, entropy always plays a role. This is why it is so useful to have a volatile "leaving group" in many reactions, so S stays roughly constant:
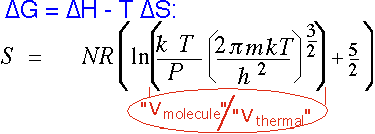
for an ideal monatomic gas. V(molecule) is the "actual" volume assigned to a molecule on the average, which is (N/V) = (kT/P) from the ideal gas law. V(thermal) is the effective zero-point "size" occupied by the molecule. Even at atmospheric pressure, this ratio is on the order of 1000 (so the natural log is around 7); in CVD we often employ pressures 100-1000 times lower, adding another factor of 3-7 in the log. Thus the contribution here is on the order of 10R/molecule, vs. typical values closer to a few R for solids and liquids.
General remark #2:
You can usually handle solid mixtures as "ideal solutions": the chemical potential is the same as that of the equilibrium vapor over the solid [which can be calculated]. The chemical potential varies linearly with mole
fraction in the solid.
In realistic situations, many overall reactions, with numerous reactants and products, need to be considered. We can treat such a situation by writing all the reactions we can think of between reactants and products. We then search for the set of concentrations which simultaneously satisfies the equilibrium constant for each reaction (or equivalently minimizes the total system free enthalpy), under the constraint that the number of each kind of atom summed over all the constituents is equal to what we "put in" to begin with. This is a problem in constrained minimization. It can be solved by standard computational methods using Lagrange multipliers. A more elegant approach is to employ element potential methods, originated by Powell and Sarner (GE Report R59/FPD (1959)) and incorporated by William Reynolds of Stanford into the program STANJAN. (In 2016, many years after I looked into this, the information still seems to be available at http://web.stanford.edu/~cantwell/AA283_Course_Material/STANJAN_write-up_by_Bill_Reynolds.pdf.)
We can classify overall CVD reactions by examining the standard enthalpy of reaction. Reactions for which the change in free enthalpy is modest are potentially reversible: the actual process may be a balance beween etching and deposition, depending on the initial conditions. Reactions involving very large changes in free enthalpy have essentially no reactants left in equilibrium: they are completely irreversible and lead only to deposition. Let's look at a few examples: shown below are some important overall CVD reactions, with the standard free enthalpy of reaction per mole of product in KJoule/mole. The reactions are given in order of increasing free enthalpy.
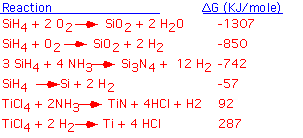
We see that the free enthalpy of reaction for the formation of silicon dioxide from silane is strongly negative. In terms of the equilibrium constant, the concentration of reactants is essentially zero in the equilibrium state: this is a highly irreversible reaction! The enthalpy release is larger when enough oxygen is available to completely oxidize the hydrogens into water. Silicon nitride formation from silane is less strongly driven, but still very much an irreversible reaction: one can't etch nitride with hydrogen.
The decomposition ("pyrolysis") of silane to form solid silicon involves a modest release of free enthalpy; it is not unreasonable to think that the reaction could be reversed, and (as we'll examine in some more detail below), this can be easily accomplished by adding a bit of chlorine to the mixture.
The deposition of TiN and Ti from titanium tetrachloride is actually not thermodynamically possible at room temperature! However, the entropy of these reactions is positive (because we're producing more high-entropy gas phase molecules than we consume). If we raise the temperature enough, the free enthalpy will become negative and the reaction will proceed: for titanium metal, temperatures in excess of 1000 °C are required. This explains the commonplace observation that it is difficult to deposit titanium metal by CVD.
An Example: Selective Silicon Deposition
Let's look in some detail at a more complex application of thermodynamic calculations to a deposition process [after R. Madar and C. Bernard, J. Vac. Sci. Tech. A8 p. 1413 (1990)]. We consider the problem of selective deposition of silicon onto exposed silicon, without deposition on the neighboring silicon dioxide.
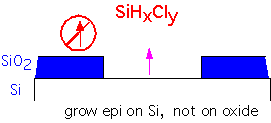
If we provide some Cl in the reactants, the free enthalpy change is small: etching reactions as well as deposition can occur, depending on the gas mixture.
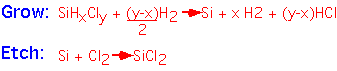
With the appropriate software and thermodynamic data, one can calculate the equilibrium concentration of various gas-phase species, and thus obtain the ratio of Si to Cl in the equilibrium mixture for any given temperature and hydrogen:chlorine ratio.
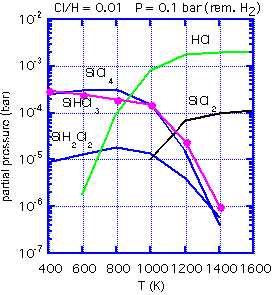
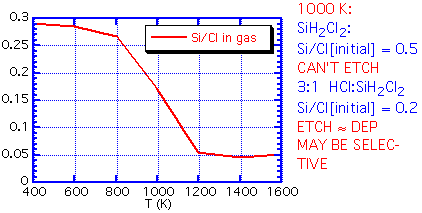
If the inlet gas has a Si:Cl ratio greater than the equilibrium ratio, no etching can occur: the path to an equilibrium composition requires a reduction in Si in the gas phase, which implies that solid silicon must be deposited. An inlet Si:Cl ratio much below equilibrium will lead to etching of any exposed silicon. At 1000 K, for example, the equilibrium Si:Cl ratio is about 0.18. Thus if we use a feed of pure dichlorosilane, with a Si:Cl ratio of 0.5:1, net deposition must result. The process is unlikely to be highly selective. However, an inlet mixture of 3:1 HCl:SiH2Cl2 will give an inlet Si:Cl ratio very near that of the equilibrium mixture. The small energy difference between polycrystalline silicon growing on oxide and the more stable epitaxial silicon can be the difference between net deposition and net etching.
Some Reference Data
It is a fair approximation to associate a specific enthalpy change with each bond in a molecule -- only fair because electrons are not in fact that localized, and the strength of interaction, as we noted, depends on the geometry of a molecule as well as the atoms that compose it. We provide below a table of some useful bond energies in KJ/mole, with which one can make a rough estimate of the enthalpy of formation of species when the measured data is not available.
bonds with hydrogen
H-H 435
H-C 414
H-N 389
H-O 464
H-Si 318
H-Cl 430
bonds with silicon
Si-O 451
Si-F 564
Si-Si 221
Si-Cl 380
bonds with carbon
C-C 347
C=C 610
C-N 305
C=N 614
C-F 484
C-O 359
C=O 735
C-Si 301
C-Cl 339
bonds with nitrogen, oxygen, fluorine
N-O 221
N-F 272
O-O 195
O=O 250
O-F 188
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
