All About Atoms
Although computational quantum chemistry has made tremendous strides in the last two decades, the classification of electronic states that arises from the only chemical system for which exact analytical solutions of the Schrodinger equation can be constructed, the hydrogen atom, is still important. In this simple case, the possible states for a single electron bound to a singly-charged positive nucleus can be described by three quantum numbers: n, which gives the number of radial nodes of the wavefunction; l, which specifies the total orbital angular momentum; and m, which specified the angular momentum projected onto the z-axis.Hydrogen and its Friends: The Simplest View of Atomic Structure
In the one-electron atom, the energies of all the states of a given "shell" are the same (the states are "degenerate", a mathematical term with no implications about their moral fiber), with binding energy relative to a free electron state varying as the square of the ratio (Z/n), where Z is the nuclear charge. (For Z=1, n=1, the binding energy is the ionization energy of hydrogen, about 13.6 eV.) The "size" of the eigenfunctions is roughly the Bohr radius, 0.5 Å, multiplied by (n2/2Z). (The shells are often denoted by letters: K corresponds to n=1, L to n=2, M to n=3, etc.)
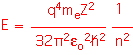

As a consequence, for more complex atoms with higher nuclear charge, the "inner" shells (small n) become very tiny and very strongly bound to the nucleus, and don't participate much in binding with other atoms. The outermost shells, with the highest values of n, "see" only the shielded nuclear charge (the actual charge minus the charge from the inner electrons), and are thus much larger and more weakly bound. It is only these "valence" electrons that can participate in binding.
The net results is that the effective "atomic radii" are smallest for atoms on the upper rows and to the right side of the periodic table, and grow larger as we move to the left and down to lower rows in the table.
Element Atomic Radius (nm)
Boron 0.088
Carbon 0.078
Oxygen 0.066
Hafnium 0.158
Tungsten 0.139
(Note that the actual wavefunctions have a complex dependence on the other quantum numbers, as well as (in larger atoms) the full electronic configuration, and can't really be summarized by a single value of the "radius". Thus these numbers are useful for discussing general trends but don't represent a true hard sphere size of a classical atom.)
The values of the angular momentum quantum number l tell us something about the "shape" of the orbitals. The various values are typically named using letters that arise from spectroscopy: l=0 is "s",l=1 is "p"l=2 is "d", l=3 is "f". There is only one "s" orbital for each shell: it is spherically symmetric. There are three p-orbitals (m=-1, 0, 1); a possible basis set has three identical orbitals oriented in orthogonal directions, known logically enough as the px, py, and pz orbitals. The d orbitals are more complex, with five possible states, and so on.
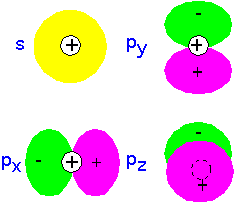
Recall that since electrons are Fermions, any given state (such as an atomic orbital) can have only two electrons, one with spin up and one with spin down: the Pauli principle. For many-electron atoms, one can imagine building an approximate state by filling up the single-electron states, each with two electrons (spin up and spin down), until all the electrons are accounted for. The result is shown below for the first row of the periodic table. Note that the p-orbitals are filled in an arbitrary manner (there's not really a preference for px over py). According to Hund's rule, we fill degenerate orbitals so as to maximize total spin (which helps keep the electrons away from each other): thus in C and N the electrons go into separate p orbitals, only pairing up (as in O) when there's no room left.

It is, however, important to note that this is only a rough approximation. The first corrections are to account for the splitting of the p orbitals away from the s orbitals in energy, while still regarding the states as non-interacting. For bigger atoms (lower in the periodic table), interactions become more and more important and it is more difficult to regard the hydrogenic wave functions as a useful basis set.
Atoms look vaguely "spherical" in most respects. It is possible to define an effective atomic radius, if you don't take it too seriously: very useful for qualitative purposes, not for three-decimal precision.
From the schematic diagram below, we see that the first row elements are quite "small”, whereas the transition metals and rare earths at the bottom left of the table are almost four times as big. This disparity enables us to think about substances like WN or WC as being materials in which the small atoms (N or C) occupy interstices between the large W: they are "interstitial" compounds. Atomic radius can be a useful approximate guide for guessing what sort of structures will occur, especially in metals where bonding is somewhat non-directional, so that one can treat the atoms as being almost close-packed spheres.
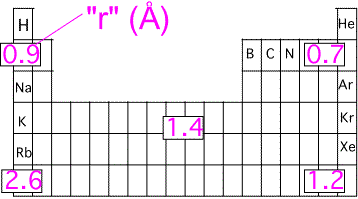
Covalent Bonds
When two atoms are located near each other, it is often the case that a change in the electronic states could lower the total energy of the system, by placing more charge in the region between the nuclei: that is, a bond can form between the atoms. The orthogonal state has zero density between the atoms: it generally has a higher energy than the atomic states and is "anti-bonding".
It is often useful to try to represent the bonding state as a linear combination of the single-electron states on the two atoms: this is the basis of the "LCAO" or Huckel molecular orbital theory. If we approximate the Hamiltonian for a two-atom system A - B as being composed of a one-electron energy and an overlap between orbitals, we find that the overlap interaction causes the electron energy levels to split into a lower (bonding) and upper (antibonding) state.
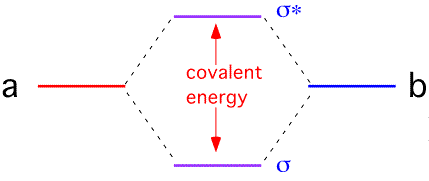
If each atom in the bond contributes one electron, both electrons go into the lower state (with, of course, opposite spins). The total energy of the system is lower than it was when the two atoms were separate; a bond has been formed. The "order" of the bond is 1 since a single bonding electron pair is present.

If each atom in the bond has two electrons to contribute, the upper (antibonding) levels must be filled. To lowest order, the energy is the same as it was when the atoms were separated; no bond results (bond order = 0).
Bonds of this sort are called covalent bonds, and are an important part of the chemistry of many substances, especially those involving the first couple of rows of the periodic table.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
