Ambipolar Diffusion
In this section we’ll take a closer look at how electrons get around in a plasma. Because the electrons and ions are charged, they are even less free than neutral molecules to move on their own: where one charge goes, the other must (mostly) follow.
Transport with Charge
Electrons and ions move with thermal velocities just like neutral molecules do; therefore diffusion plays a role in where they end up. However, the two sorts of species don't move independently: the motion of electrons creates a charge imbalance and a resulting electric field that drags the ions along with them.
Let's look at how to incorporate this fact into our existing knowledge of mass diffusion. The total flux of charged species such as electrons and ions is composed of a drift component and a diffusion component. The drift flux is that driven by the electric field; it is of the form (mobility)*(density)*(electric field), and is of opposite sign for electrons and ions. The diffusion component is that which we are familiar with: a diffusion coefficient multiplied by the negative gradient of concentration. Thus we can write expressions for the flux of ions and electrons in the plasma. Note that here D’s are the diffusion coefficients, and μ’s are the mobilities (ratio of electron or ion motion to electric field).
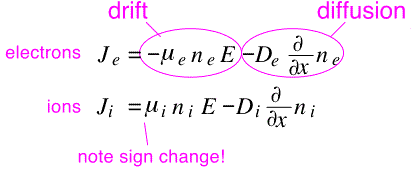
Now we make an important approximation: we assume that imbalances in the fluxes and densities are very small. Thus we can take the ion and electron densities to be equal, and require that the ion and electron fluxes be equal. After a bit of algebra we obtain an expression for the electric field:
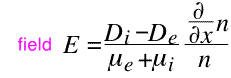
We then substitute this field into either of the flux equations to get an expression for the flux in terms of the density. Note that in the drift term, the "n's" cancel: both the terms end up being proportional to the gradient dn/dx.

We thus end up with an expression in which the flux of charged species J is simply proportional to the negative gradient of the concentration: that is, we're back to a simple diffusion equation, but with a new ambipolar diffusion coefficient Da.
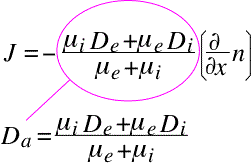
The form of Da can be simplified by first noting that the mobility of the electrons is usually much larger than that of the ions. We can ignore the ion mobility in the denominator, obtaining:
This expression can be re-expressed in terms of more convenient parameters by using the Einstein relation

resulting in the most common form:
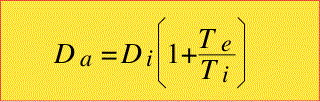
In the same fashion as in conventional mass transport, this leads to a diffusion equation:

We find that the diffusion coefficient is essentially that of the ions multiplied by the ratio of electron and ion temperatures. The diffusivity of the ions will be of similar magnitude to that of neutral molecules. Recall that at atmospheric pressure these values were typically around 0.1 cm2/sec, so at e.g. pressures of 1 Torr, diffusivity values of 75 cm2/sec are reasonable. For typical plasmas the electron temperature is around 3-5 eV and the ion temperature perhaps 0.05-0.1 eV, so the multiplier Te/Ti is about 50-100. Thus reasonable values of ambipolar diffusivity are 3500 to 7500 cm2/sec at 1 Torr.
Let's look at what this implies for the transport of electrons and ions in a fairly typical sort of plasma chamber: a cylinder 50 cm in diameter and 5 cm high, operating at 1 Torr, with a typical Da = 5000 cm2/sec. [As usual, we use the ideal gas law, and make the simplifying assumption that the gases are near enough to room temperature that we can ignore thermal expansion. If you're puzzled by the table, see the Introduction and the discussion of diffusion length in Transport. ]

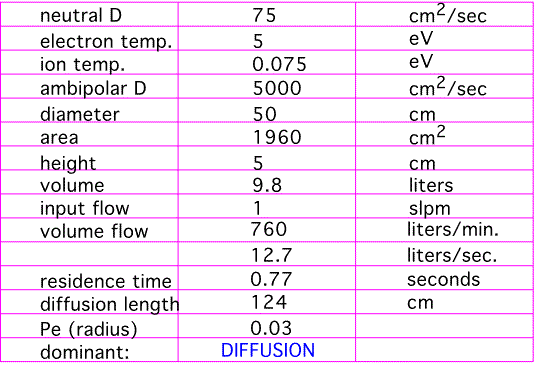
We see that the ambipolar diffusion length greatly exceeds the chamber size. Electrons and ions diffuse very rapidly, and at typical values of gas flow velocity convection is not important in determining where the charged species go. This is very convenient for analyzing what's going on in the reactor: we can treat the plasma behavior while ignoring any flow velocity of the gas, and then treat the transport of species with the plasma providing a mechanism for generating stuff in the gas phase, without trying to intimately couple them together.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
