Complex Exponentials: a quick review
Daniel M. Dobkin
The complex exponential exp(ix) or for electrical engineers exp(jx) is a nearly unavoidable beast in the analog side of electrical engineering and wave propagation. The young Richard Feynman found the concept a remarkable mathematical revelation; current readers may differ, but it is very helpful to become comfortable with complex harmonic quantities in this field. So let's start.
To begin, let's review complex numbers. Complex numbers are defined as numbers that contain an imaginary component. The basic imaginary number, i, is a number which when multiplied by itself produces (-1): that is, i*i = -1. This idea gave algebraists in 14th-century Italy serious headaches but it needn't trouble the modern reader: integers and real numbers are just constructs that obey rules, so imaginary numbers and their complex cousins are no different. You just need to learn the rules.
A pure imaginary number is any multiple of i : 2i , -5i , and 63.7599342551i are examples. A complex number is the sum of a regular old real number and an imaginary number: 2.5 + 11i is complex. Complex numbers were introduced in order to solve certain algebraic equations, but that's not why they are interesting to electrical engineers.
The really neat part about complex quantities is that they can be depicted on the complex plane. If you draw a plane with the horizontal axis representing real numbers and the vertical axis representing imaginary numbers, a particular complex number corresponds to a particular spot in the plane:
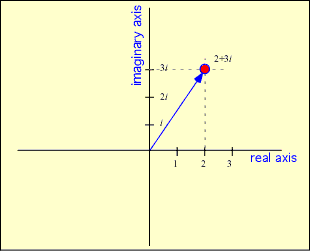
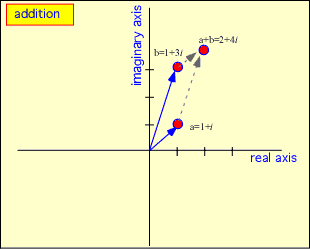
Algebraic operations can then be shown pictorially. Addition corresponds to conventional vector addition: you grab one of the arrows (say a) and move it until the base sits on the other point (b); the point of the transported a then indicates the sum of the two complex quantities:
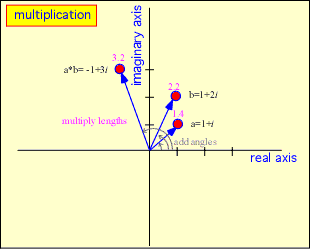
To multiply two complex numbers you can multiply their coordinates together, remembering that i*i = -1, or just multiply their lengths and add their angles.
We can define the complex exponential: exp(ix) = cos(x) + i*sin(x). Since the cosine and sine are just the horizontal and vertical distances -- that is, the coordinates -- corresponding to an angle x, any complex number can be represented as an exponential of its angle, multiplied by the length. Using the usual rule for multiplying exponents, exp(a) * exp(b) = exp(a+b) we get back the rule for complex multiplication given above.
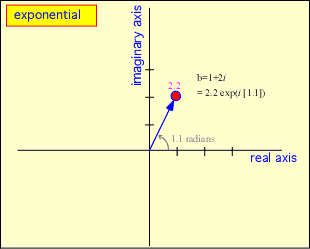
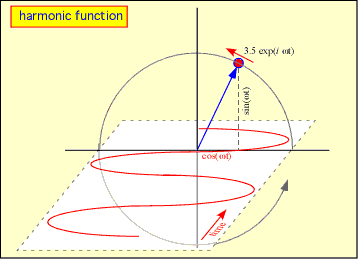
Now the nifty part. If the argument of the exponential (the ix part) is made proportional to time, a = exp(iωt) [here ω is the frequency in radians per second; divide by 2π to get the frequency in Hertz] the complex vector runs around in a circle in the complex plane, with its real and imaginary parts describing cosines and sines respectively of time. Adding something to the argument is equivalent to imposing a phase shift, and since adding in the argument is like multiplying by a complex number, we get a very elegant way of expressing any arbitrary harmonic function of time, including phase shifts and amplitudes.
What you do with the complex number is itself complex and not entirely consistent. In electromagnetism, the complex value is often considered to be a convenient manipulative trick, where you take only the real part when you're done. In engineering, the final real voltage is often obtained by adding up a sinusoidal signal proportional to the imaginary part of a complex voltage to a cosine proportional to the real part; these are frequently known as "I" (cosine) and "Q" (sine) for in-phase and quadrature (why would you expect "I" to stand for imaginary? now really, that would be too easy). It's not always obvious what convention is being adopted. We'll try to let you know.
